Práctica 8. Movimiento circular y aceleración centrípeta

Fuerza centrípeta

Mediante este experimento de física podrás determinar la fuerza centrípeta de un cuerpo que gira en movimiento circular uniforme. Se experimentara con dos métodos para calcular dicha fuerza. En uno deberás medir distancias con una regla, en el otro contar vueltas.

En la conclusión deberás comparar los resultados obtenidos, por ambos métodos y describir como se complementan.

Objetivos

Que los alumnos:

• Comprendan la acción de la fuerza centrípeta que actúa sobre un cuerpo en movimiento circular uniforme.
• Utilicen métodos experimentales para estudiar fenómenos físicos.

Descripción

En esta actividad, los alumnos realizarán un experimento cuyas variables pueden ser controladas para poder observar y analizar un fenómeno físico. En este caso, el movimiento circular y la fuerza centrípeta.

Fuerza centrípeta

En el movimiento circular uniforme, un cuerpo se mueve en una trayectoria circular a una velocidad de desplazamiento constante. Este movimiento es el que describe, por ejemplo, una piedra a la que hacemos girar atada a una soga. Si la hacemos girar más rápidamente, debemos agarrar la soga con mayor fuerza para que no se deslice de la mano permitiendo que la piedra se aleje y gire con un radio mayor. Da la sensación de que sobre la piedra actúa una fuerza que «la jala hacia afuera», a esta le llamamos fuerza centrífuga. Sin embargo, esta «fuerza centrífuga» en realidad no existe, ya que sobre la piedra actúa una fuerza que «la jala hacia adentro», en la dirección de la soga. Esta es la fuerza centrípeta.

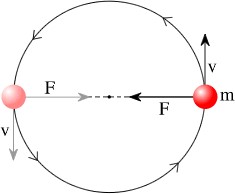
Un cuerpo de masa m en movimiento circular uniforme de velocidad v y fuerza centrípeta F.

La fuerza centrípeta (F_c) necesaria para producir este movimiento debe tener una magnitud que depende de la velocidad de desplazamiento o rapidez (v), del radio de rotación (r) y de la masa del cuerpo (m):

F_c = m v²/ r

Si la velocidad es mayor o el radio de rotación es menor, la fuerza centrípeta que mantiene el movimiento circular debe ser mayor. En el caso de que la fuerza hacia el centro sea insuficiente, entonces el cuerpo tenderá a alejarse, creando la sensación de que actúa una fuerza (centrífuga) hacia afuera.

Si la fuerza centrípeta F desaparece, el cuerpo se desplaza con movimiento rectilíneo uniforme.

           

Método 1.

Con este método vas a obtener la fuerza centrípeta de un cuerpo giratorio de masa conocida midiendo distancias con una regla. Para hacerlo necesitarás un aparato armado como en la figura:

  Materiales

·         Sistema rotacional con motor para variar la velocidad.

·         Riel de aluminio de 50 cm de largo.

·         2 pesas de masa conocida (de 20 a 50 gramos) atada a un hilo de y que cuelguen del sistema rotacional aproximadamente 20 cm (péndulo).

·         Flexómetro

·         Escuadra (lo trae el alumno)

·         Hoja de papel cuadriculado (lo trae el alumno)

 

Armado del aparato

Antes de realizar la medición debe armarse un aparato de acuerdo a las figura,

1.    Haciendo girar el motor a baja velocidad verifica que el sistema gire sin vibrar.

2.    Cuelga el péndulo de uno de los extremos de la varilla.

3.    Con el sistema en reposo pega la hoja de papel sobre la mesa, deben estar separadas por lo menos medio centímetro.

4.    Marca el punto donde se encuentra la pesa, y gira manualmente el sistema para ver que la segunda pesa pase también por la misma marca.

La medición

1.    Hacer funcionar el motor en su velocidad mínima y deja que se estabilice el sistema. Al girar, el péndulo se inclinará hacia afuera, alejándose una distancia d de la posición vertical inicial, formando un ángulo.

2.    Mide la distancia d, apoyando una escuadra sobre la mesa.

En esas condiciones realiza las mediciones necesarias para el análisis dinámico de la pesa, masa, que gira.

3.    Toma la medida de la distancia d, que es la diferencia entre las dos marcas que indican las posiciones de la escuadra.

4.    Calculá el ángulo  utilizando los valores de L y d que obtuviste.

5.    Calculá la fuerza centrípeta  utilizando el análisis de fuerzas y los valores del peso P y el ángulo .

6.    Repite la medición varias veces y calcula la fuerza centrípeta como el promedio de los valores hallados.

7.- Cambia las pesas por otra de diferente masa y repite el experimento. Justifica tus resultados con la teoría y tus datos.

Cálculo de la fuerza centrípeta

En el experimento, cuando la rotación es más rápida, la pesa tiende a alejarse del centro. Para explicar lo que ocurre consideremos el siguiente esquema.

El peso de la esfera P puede ser descompuesto en un paralelogramo de fuerzas, en el cual la fuerza T tiene la dirección de la soga y la fuerza F es radial (hacia el centro). La fuerza T es equilibrada por la tensión de la soga (no dibujada en el esquema), según el principio de acción y reacción. La tensión tiene la misma magnitud, pero el sentido inverso a T.

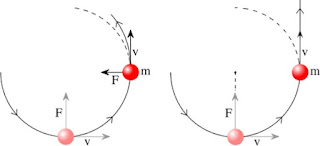
En cambio, la fuerza F no está equilibrada. Una fuerza no equilibrada, según el principio de masa, produce una aceleración en su misma dirección y sentido. Luego, la fuerza F acelerará la esfera hacia el centro de la rotación, actuando como una fuerza centrípeta de un movimiento que cambia constantemente de dirección. La dirección de F es perpendicular al vector velocidad, que es tangencial a la trayectoria circular (línea punteada). Si se cortara la soga, la fuerza centrípeta que ella genera desaparecería, y la esfera se movería en una línea recta tangente a la trayectoria circular que llevaba.

¿Qué sucede si aumentamos la velocidad de rotación?

La velocidad angular de rotación (ω) corresponde al ángulo tomado desde el centro de rotación, que cubre el móvil en un segundo. La rapidez tangencial (v_t) depende de la velocidad angular y del radio (r): 

Si aumentamos la velocidad angular de rotación, también aumenta la rapidez (v_t) del movimiento circular uniforme.

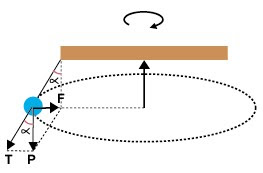
Al aumentar la rapidez tangencial, será necesaria una fuerza centrípeta mayor para hacerla cambiar de dirección y mantener el movimiento circular. En el esquema puede apreciarse que F y P dependen del ángulo (α) de inclinación del péndulo. Su relación es:

Por lo tanto:                

De la última ecuación deducimos que para que aumente F debe aumentar α, ya que P es el peso de la esfera, y es constante.

Entonces, para que aumente la velocidad de rotación es necesaria una fuerza centrípeta mayor. El incremento de la fuerza centrípeta se logra con el incremento del ángulo α . Al aumentar el ángulo, la soga gira en una posición más horizontal, con la pesa más elevada y alejada del centro. De esta manera, parece que hay una mayor fuerza «hacia afuera» cuando en realidad actúa una fuerza «hacia adentro» que hace cambiar de dirección al vector velocidad.

Método 2. Contamos las vueltas

Con este método se calcula la fuerza centrípeta utilizando la velocidad angular del movimiento circular. Para hacerlo necesitas el mismo aparato que para el método 1 y un cronómetro.

Cálculos necesarios

La velocidad angular (ω ) es el ángulo (en radianes, 1 vuelta = 2π= 6,28) que barre el cuerpo en una unidad de tiempo (1 segundo). Se puede calcular a partir del tiempo (t) que tarda el cuerpo en dar un determinado número (n) de vueltas o revoluciones:

Por ejemplo, si tarda 70,8 s para dar 40 revoluciones, la velocidad angular es:

Para calcular la fuerza centrípeta por este método aplicamos la fórmula:

m es la masa de la pesa, R es la distancia entre el extremo de la varilla y el eje de rotación (ver figura del método 1), y d es la distancia en la que el péndulo se desvía de la posición vertical, medida en el método 1. Las unidades son las siguientes:  

El resultado Fc es en newtons.

La medición

1.    Haga girar el motor a una velocidad razonable para que puedan ser contadas las revoluciones.
Atención: las velocidades de rotación del método 1 deben ser iguales a las del método 2 para poder comparar las fuerzas centrípetas obtenidas.

2.    Cuando el motor alcance una velocidad constante, comenzá, al mismo tiempo, a contar vueltas y a registrar el tiempo con el cronómetro.

3.    Después de un cierto número de vueltas (n), por ejemplo 50, detené el cronómetro.

4.    Con el tiempo (t) registrado y n, calculá la velocidad angular (ω) (como en el ejemplo que te presentamos) y luego la fuerza centrípeta.

5.    Calculá la fuerza centrípeta utilizando m, ω , R y d con la fórmula: .

6.    si en nuestro sistema giratorio ponemos un plano inclinado y sobre este un carrito, ¿que podríamos calcular para esto? y ¿Cómo diseñarías esta parte del experimento?

 

Orientaciones didácticas

Incluye los siguientes contenidos:

• Fuerzas y movimiento: movimiento circular uniforme, fuerza centrípeta.
• Análisis del funcionamiento de objetos tecnológicos y sistemas naturales que involucren fenómenos gravitatorios.

Sugerencias

• Este experimento lo puedes realizar en casa con un ventilador que gire lento o con un viejo tocadiscos con una varilla fija sobre el plato.
• Se puede repetir la experiencia modificando la distancia al centro de rotación o modificando la velocidad de rotación. Estas variaciones pueden analizarse mediante representaciones gráficas de los resultados.
• Si se utilizan los dos métodos de medición, se puede proponer a los alumnos que comparen los resultados, expliquen las diferencias, discutan las posibles fuentes de error experimental y sugieran cómo reducirlo.

Bibliografía

• Wilson, Jerry D., Física, México, Prentice Hall Hispanoamericana, 1994.
• Serway, Raymond A., Física, México, Mc-Graw-Hill, 1993.
• Sears, F. y M. Zemansky, Física, Madrid, Aguilar, 1966.
  
  

Recordemos que, por el principio de inercia, un cuerpo se mueve en línea recta y con velocidad constante cuando la resultante de todas las fuerzas que actúan sobre él es nula. Cuando las fuerzas no se anulan, la fuerza resultante produce una aceleración, es decir, una variación de la velocidad. Como la velocidad es un vector, se puede variar de dos maneras:

         Modificando su magnitud o módulo (en el caso del vector velocidad, decimos que variamos su rapidez). Para hacerlo, la fuerza resultante debe tener la misma dirección que el vector velocidad.

         Alterando la dirección del vector velocidad (cambia la trayectoria sin variar la rapidez). En este caso, la fuerza resultante debe ser perpendicular al vector.

Una fuerza que tenga una dirección diferente de la velocidad, pero que no es perpendicular a la misma, modifica ambas: la rapidez y la dirección. En este caso, la fuerza puede ser considerada como la suma de dos fuerzas perpendiculares: una en la dirección del movimiento y otra en dirección perpendicular, según su descomposición en un paralelogramo de fuerzas.

Entonces, para que un cuerpo describa un movimiento circular uniforme debe actuar una fuerza –la fuerza centrípeta– que actúe perpendicularmente en dirección al centro de rotación, desviando el cuerpo de su recorrido rectilíneo.